「不動小数点数」は コンピュータにおいて、1 と 0 だけでマイナス符号や小数点がある数を表現する方法です。
以下に詳しくみていきましょう。
10進法での浮動小数点数の表し方
まずは、馴染みのある10進法で、「浮動小数点数」の表し方をみてみましょう。
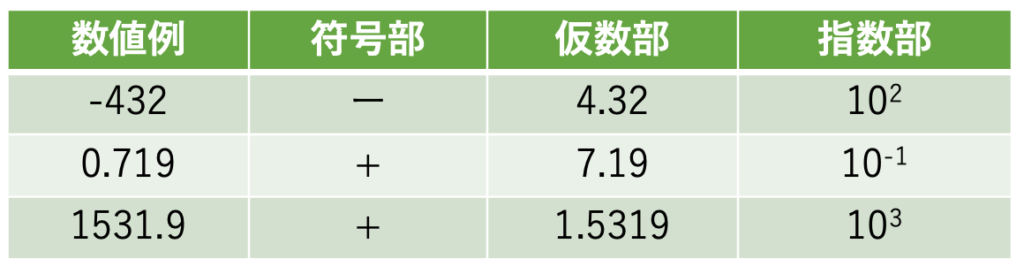
上の表では3つの実数(-432、0.719 および 1531.9)を、「浮動小数点数」として表しています。
ここで大事なことは、「浮動小数点数」は、「符号部」、「仮数部」および「指数部」に分けて考えるということです。
「符号部」:+(プラス)か ー(マイナス)かを表す
「仮数部」:最上位の桁が、1の位になるように調整した少数
「指数部」:仮数部を元の数に戻すために必要な10の何乗の形(=仮数部の小数点を動かした数)
2新法での浮動小数点数の表し方
それでは、コンピュータで実際に使用される2進法で「浮動小数点数」を表す様子をみていきます。
例として -9.875(10) を 符号部 1bit、仮数部 23 bit、指数部 8bit (合計32 bit)で表してみます。ちなみに、この表現方法は「IEEE(米国電子電気技術者協会)」によって規格化された形式です。
まず、9(10)を 2進数に直すと、1001(2) となります。
求め方は、以下のように対象とする数を 2 で割っていき、最後の商が1になったら終わり。
9/2 = 4 余り1
4/2 = 2 余り0
2/2 = 1 余り0
そして、最後の商と、余りを下から順に並べていくと1001(2) となります。
一方で、0.875(10) は0.111(2) となります。
(小数の2進数への変換は少し、ややこしいので別のページで紹介します。)
よって、 -9.875(10) = 1001.111(2) となります。
さて、この2進数をまずは指数表記に直していきます。
指数表記では、仮数部を 最上位の桁が、1の位になるように調整します。
よって 1001.111(2) は、 1.001111 x 23(2) となります(2進数なので、底は10 ではなく2であることに注意しましょう)。
さて、ここで実際に 32bit 中に、どのように並べていくかを確認していきます。

順序は、符号 → 指数部 → 仮数部 となっています。
・符号部には、正の場合は「0」、負の場合は「1」を入れます。
よって、今回は負の値ですので「1」が入ります。
・指数部は、特殊で、127(10) = 01111111(2)を足して表示することになっています。
これは、この方法での表現範囲である -127乗から 128乗までを 0から255までの正の値で表現することを意味しています。
よって今回の例では 3(10) + 127(10) = 00000011(2)+ 01111111(2) = 10000010(2) を入れることになります。
・最後に仮数部は、1を除いた、 001111(2) を入れますが、23bit ですので、余った分は 0 で埋めます。
よって、 00111100000000000000000(2) を入れることになります。
最終的に、 -9.875(10) を(IEEE754形式の)32ビットの浮動小数点数にした値は、
「1 1 0 0 0 0 0 1 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 」となりました。
