コンピュータの内部で使われる数字は「0」と「1」のみ、つまり 2進数が使われます。これは簡単に言えば、電流が流れていれば「1」そうでなければ「0」であるとすることが単純に実現できるからです。ここでは、その2進数の計算が行われる仕組みをみていきましょう。
コンピュータは電気回路を持ち、その回路の中でも演算や制御を行う回路を「論理回路」といいます。まずは、その「論理回路」(「論理積回路(AND回路)」、「論理和回路(OR回路)」そして「否定回路(NOT回路)」)をみてきましょう。
論理積回路(AND回路)
「AND回路」は、2つの入力と1つの出力を持つ回路です。2つの入力を (A), (B) とし、 1つの出力を (C) とすると、この回路は以下の表の通りに「2つの入力が共に1の場合のみ1を出力する」ように決められています。
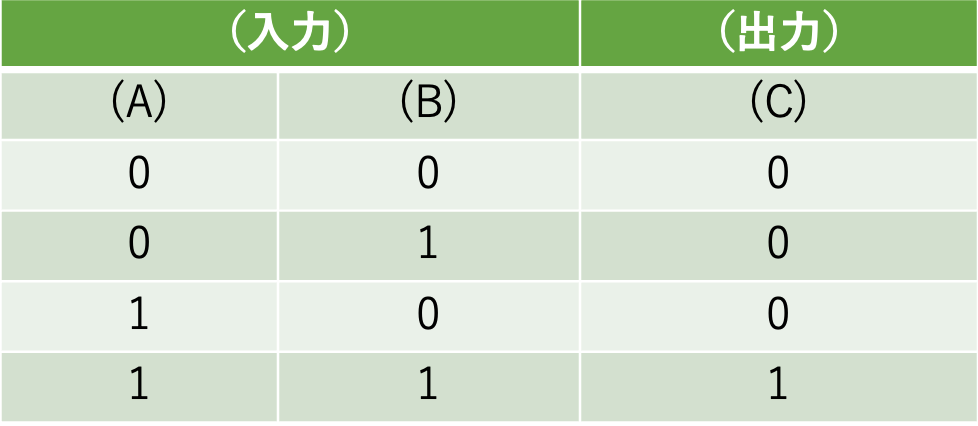
上の表を良く見てみると (A) x (B) = (C) の関係になっている事が分かります。「論理積」は「積」の関係になっていますね。
論理和回路(OR回路)
「OR回路」にも、2つの入力と1つの出力があります。上と同様に、2つの入力を (A), (B) とし、 1つの出力を (C) とすると、この回路は以下の表のとおりに「入力のいずれか一方に1があれば、1を出力する」ように決められています。
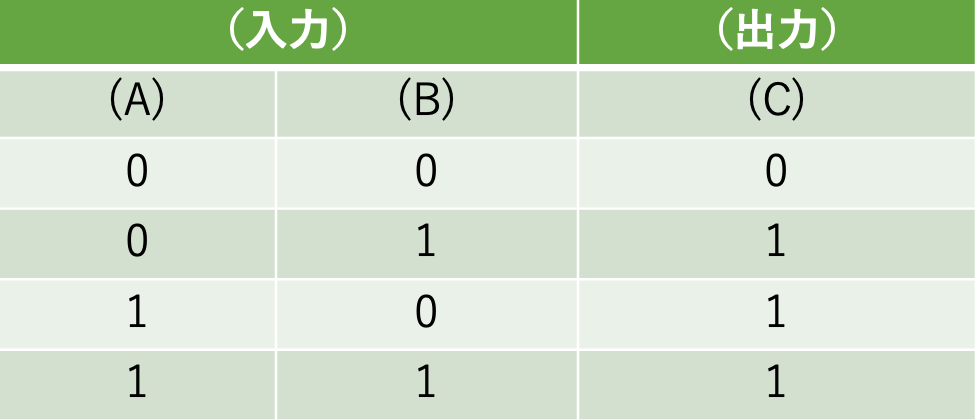
入力に 1がひとつでもあれば、1を出力していますね。
否定回路(NOT回路)
「 NOT回路」は、1つの入力と1つの出力からなります。「否定」の名のとおり、「入力した信号を反転して出力する」ように決められています。
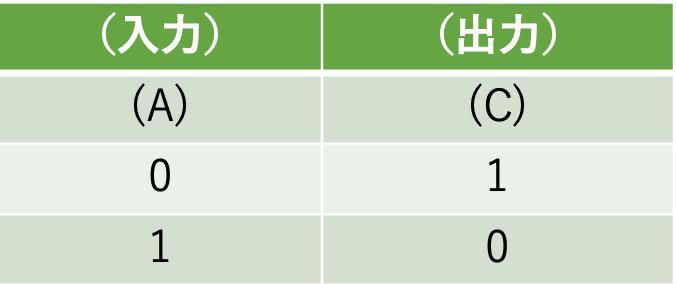
とても単純ですね。
以上3つの「論理回路」を組み合わせることで、2進数の演算(計算)ができるようになります。
論理回路の図記号
先に述べたように、実際に2進数の演算では複数の「論理回路」を使用します。そのため、図を使った説明が理解を助けます。
そこで、以下に使われる記号を図示します。
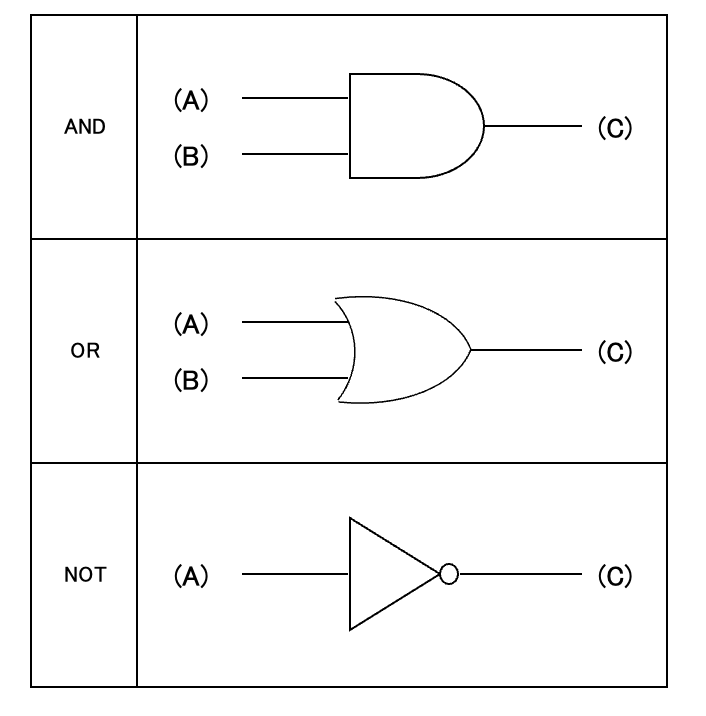
電気回路っぽい表記になっている感じがしますね。
二進数の足し算(加算):半加算回路
それでは、実際に論理回路で「二進数の足し算(加算)」を実現する回路(半加算回路と呼ばれます)を説明します。
まず、はじめに2進数の足し算について確認します。
下の表が2進数の加算の結果で、 (A) +(B) =(C) のかたちで表しています。
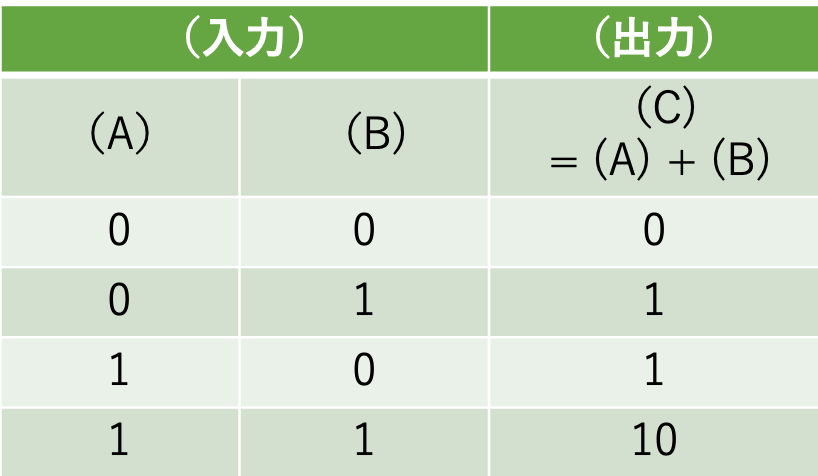
0 と 0 の足し算の結果は 0 で、0 と 1(同様に1 と 0) の足し算の結果は 1 です。これは、10進数の場合と同じでとても慣れている計算かと思います。
一方で、1 と 1 の足し算の結果が 10 になる部分が慣れない部分です。2進数においては、各桁は 0 か 1 しか表す事ができないというルールがあります。
ですので、10進数の 2 にあたる部分は「桁上がり」で表現されることになります。
よって、「二進数の足し算(加算)」を実現する「半加算回路」では、入力(A)および(B)がそれぞれ1桁でも、出力は2桁分を用意しなくてはならないことが分かりますね。
そこで、上の表の出力部を2桁に対応した形に書き換えてみます。
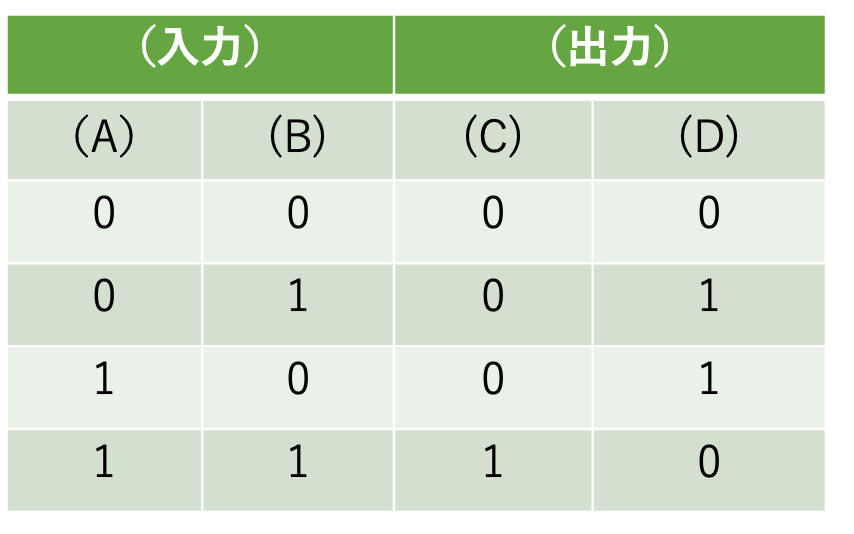
(出力)部の(D)が1桁目を、(C)が2桁目を表しています。
それでは、実際の「半加算回路」を見ていきます。下の図が全体図です。
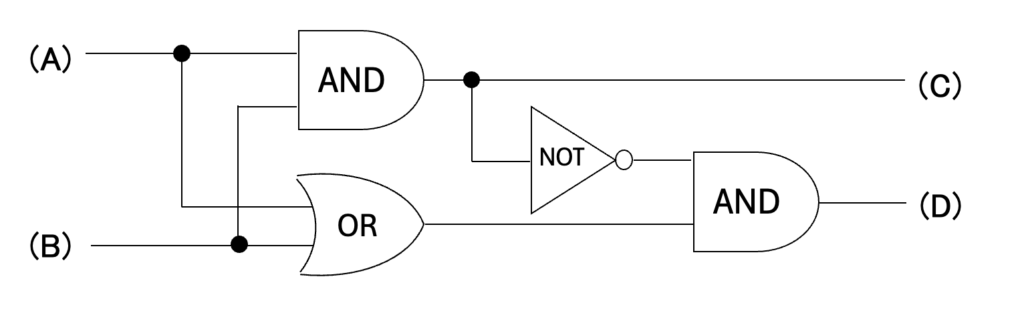
「AND回路」を2個、「OR回路」、「NOT回路」を各々1個、合計4個の「論理回路」が使われています。
また、回路中の ● の部分は、データが分岐し、それぞれに同じデータが流れて行くことを示しています。
よって、(A)および(B)に入力させたデータは、初めの「AND回路」、「OR」回路のどちらにも流れています。
より詳しくみていくと、まず(A)と(B)からの入力を受けっとた「AND回路」は、(C)に直接出力しています。(C)は2桁目に対する出力でした。(A)= 1、(B)= 1 の場合にのみ、(C)への桁上がりが発生しますので、「AND回路」で表現できることが分かりますね。
一方で、1桁目に対する処理は少し複雑です。まず、入力データは「OR回路」を通ります。よって入力(A)または(B)のどちらか一方でも 1 があれば、その「OR回路」は 1を出力します。そして、それを次の「AND回路」に渡します。また、その「AND回路」のもう一つの入力として、2桁目の出力に使用した値を、「NOT回路」で反転させて使っています。この処理は桁上がりをした((C) の出力が1となった)のならば0を受け取ることになります。桁上がりをすると1桁目は 0になる必要があります。よって、(D)への出力のための「AND回路」の入力に0が一つでも含まれれば 、その「AND回路」は 0 を出力しますので、理にかなっていますね。また、「NOT回路」による反転で1を受け取った(桁上がりが発生しなかった)場合では、その前の「OR回路」から1が出力されれば、(D)に1を出力し、0が入力されれば、0を出力します。
以上が「半加算回路」の説明です。じっくりと図をたどってみましょう。
また、この加算ができれば、掛け算もできることになります。なぜなら n x m という演算は、n を m 回足しこむことで実現できるからです。
さらに、引き算が実現できれば、割り算も実現できます。引き算については少し複雑さが増しますので別の機会に説明したいと思います。
