相関関係
問題解決(理想の状態と現状のギャップを解消する行為)のため、既知のデータを解析し、何かしらの法則や関係性を見つけだす行為が実社会では多く行われています。ここでは、ある変数Aと別の変数Bについての関係性を調査する前提で以下をすすめていきます。
相関関係
変数Aと変数Bと関係性を示すのが「相関関係」です。お互いの変数がどのように関わっているのかを調査したものです。以下に具体例を示していきます。
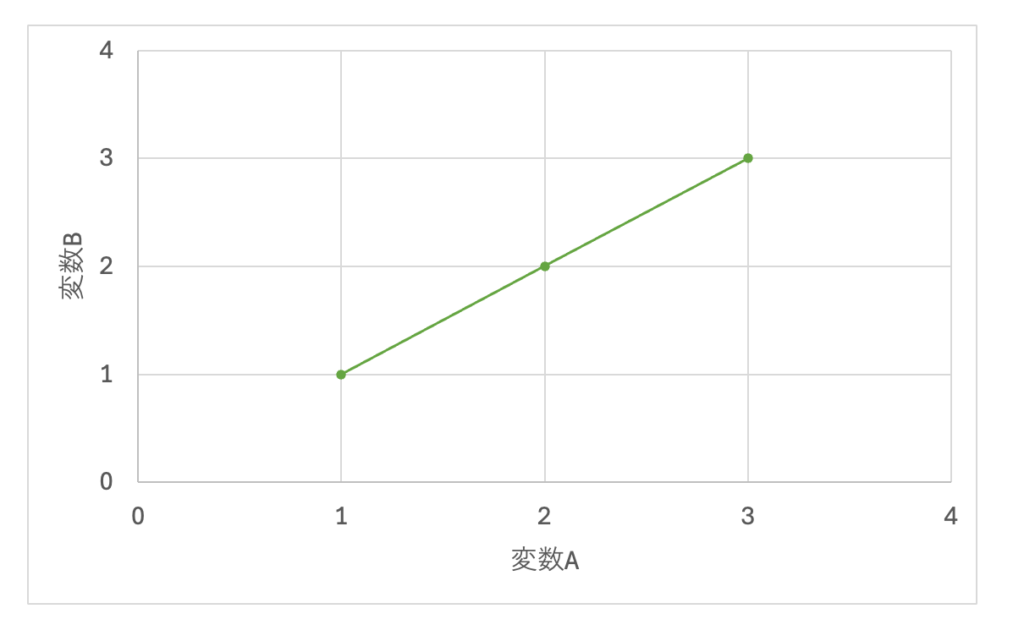
上のグラフでは、3点がプロットされており、それを線で結んでいます。その3点を詳しくみると、変数A = 1 のとき 変数 B = 1、変数A = 2 のとき 変数 B = 2、そして 変数A = 3 のとき 変数 B = 3 となっています。明らかに、変数Aが増えた場合に変数Bも増えていますね。このような関係を「正の相関」があると言います。ここで注意したいのは、「変数Bが増えた場合に、変数Aも増えている」とも言えることです。このグラフのみでは、どちらがどちらに影響を及ぼしているかは断定できませんよね。
それでは、次のグラフはどうでしょうか?
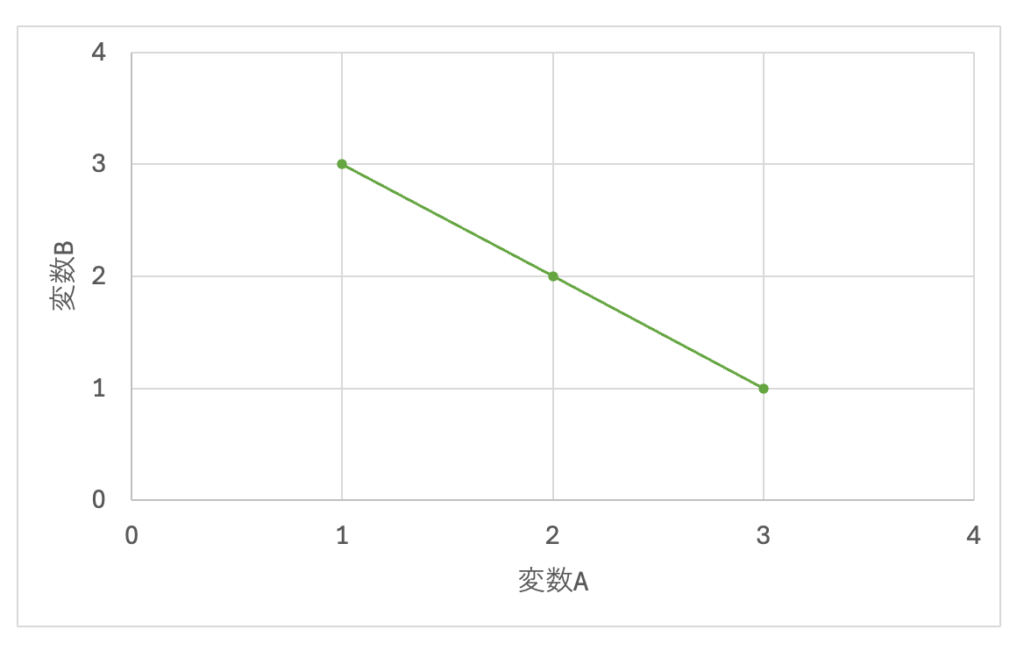
このグラフでは、変数Aが増えるにつれ変数Bが減っています(もちろん変数Bが減るにつれ変数Aが増えている、とも言えます)。この場合に、2変数間に関係性がない訳ではなく、しっかりとした関係性が存在しますね。このような場合は「負の相関」があると言います。
それでは、2変数間に関係がない場合はどのようなグラフになるかと言うと、
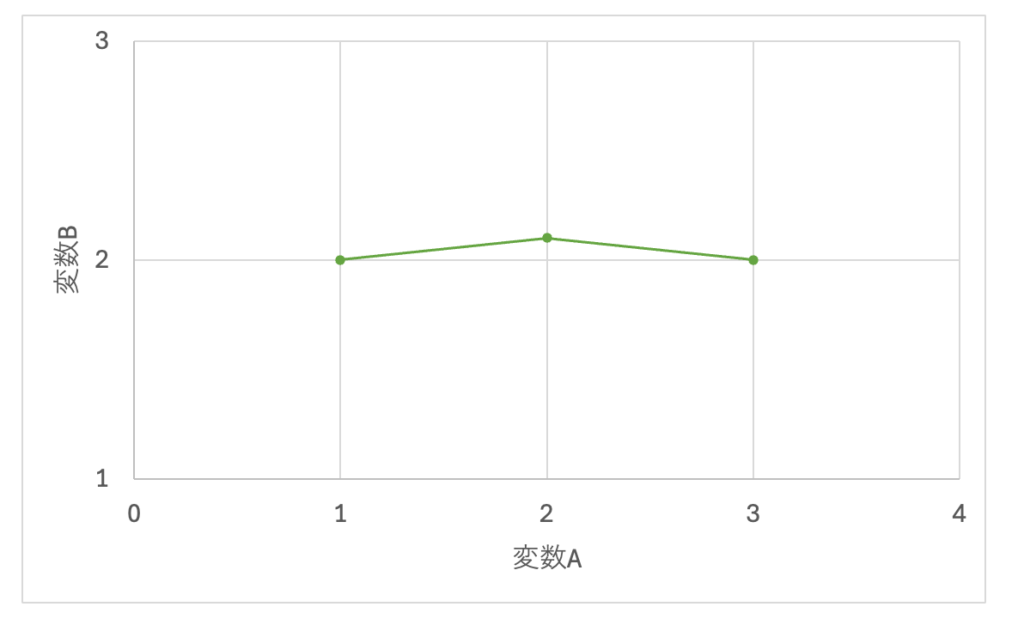
このようになります。変数Aが増えても変数Bは2近辺から変化していません(変数Bは一定でも、変数Aは変化します)。これが、「相関がない」ケースです。
相関関係はその程度の強さを「相関係数」という係数を計算で求めあらわします。それは、分散(共分散)と標準偏差から算出されるもので、取り得る範囲は -1 から 1の間です。よって、-1 が強い負の相関があり、1が強い正の相関があることになります。よって相関がない場合の相関係数は0に近づきます。
それでは最後に、以下の2つのグラフではどちらが強い相関を持つでしょうか?
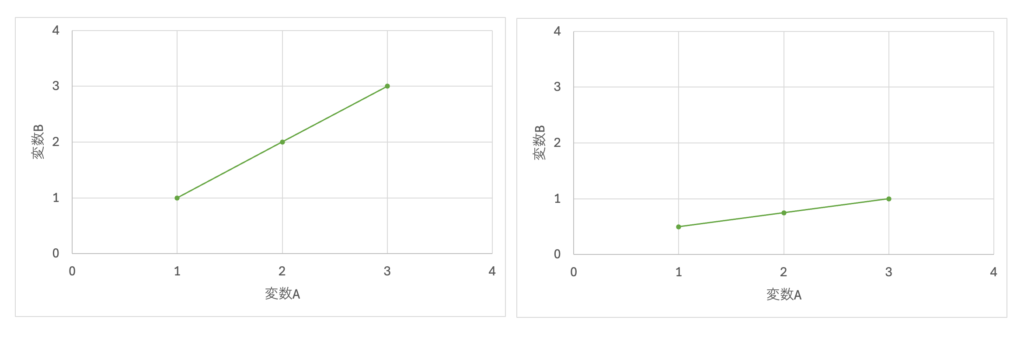
答えは、どちらも同じ 相関係数 = 1です。傾きが異なるので、左のグラフの方が派手に見えますが、先ほど述べたように相関係数の算出では共分散を用います。その共分散ではデータの平均値を用いるため、データ内の相対関係が大事になってくるのです。
擬似相関
相関係数は、上に述べたように計算で算出されます。
この時に気を付けたいのが、「擬似相関」と呼ばれる、本当はあまり関係がないのに相関係数上では関係があるように見えるものです。
例としては、
・気温が上がるとアイスクリームが売れる
・同じく、気温が上がるとビールが売れる
という、それぞれ正の相関を持つデータがあったとします。
この場合に、アイスクリームとビールの相関係数を算出すると、恐らく正の相関が見られます。つまり、「アイスクリームが売れるとビールが売れる」という関係があるようにみえるのです。一般的に、その2つは独立した関係にあり、あくまで気温がその関係の鍵を握っていますよね。
よって、相関関係を考える際には、その根拠についても注意深く考察する必要があります。
また相関係数だけに頼ると、本来は関係があるのにない、誤って関係がないとみなしてしまう場合もあります。
下のグラフをみてください。
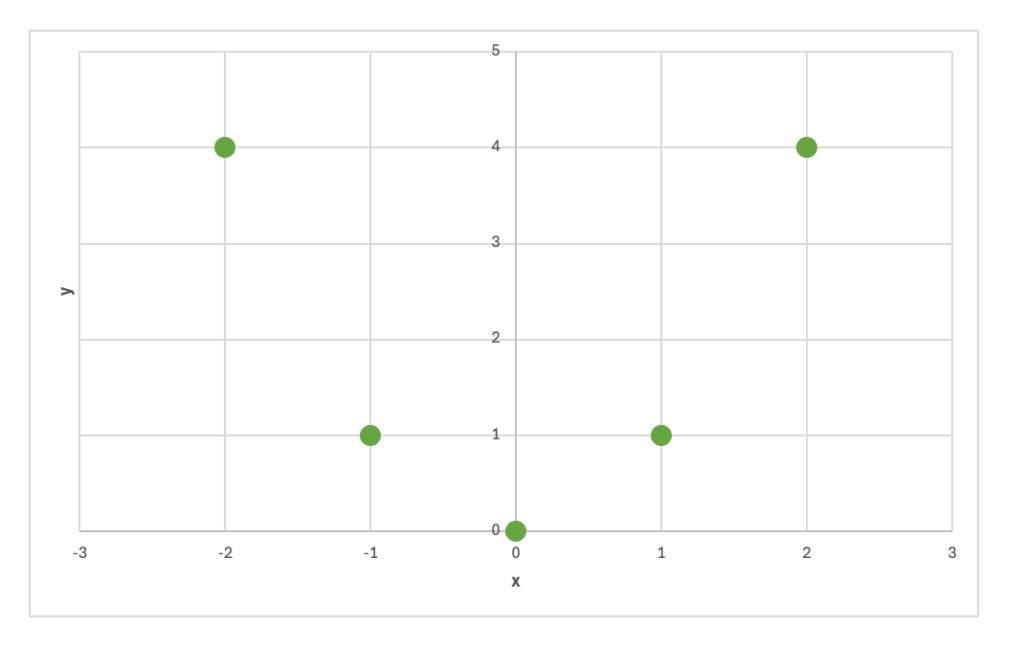
このグラフは、変数x および 変数y の関係をプロットしたものです。
これについて、相関係数を計算すると 0 となり、まったく関係がないことになります。しかしこのグラフは 式 y = x2 についてプロットしたものであり、厳密な関係が存在します。このような場合に、相関係数で判断すると 変数x および 変数y について関係がないと誤った認識をしてしまいます。
因果関係
相関関係の中でも、どちらかの変数がもう一方の変数に影響している関係を「因果関係」と呼びます。
例としては、「(A)冬の気温が例年より低くなると、(B)ダウンジャケットが売れる」などです。
この「因果関係」で大事なことは、A → B という方向性があるということです。つまり、B → Aは成り立ちません。
(B)ダウンジャケットが売れると、(A)冬の気温が例年より低くなる のはおかしいですよね。

