LeetCodeに挑戦:DP系問題 Medium (その4)
今回は、LeetCode の難易度・Mediumの問題の中で、動的計画法(DP)を使うことのできる問題、
516. Longest Palindromic Subsequence を解いてみます。
(問題)
文字列 s が与えらます。その s の中で、回文で最長となる部分列をみつけなさい。文字列 s の長さは最大で1000 です。
(例1)
Input: “bbbab”
Output: 4
説明:回文で、最長となる部分列は “bbbb” です。
(例2)
Input: “cbbd”
Output: 2
説明:回文で最長となる部分列は “bb” です。
解答例を以下に示します。
class Solution:
def longestPalindromeSubseq(self, s: str) -> int:
#(1)
n = len(s)
#(2)
dp = [ [0] * n for _ in range(n) ]
for i in range(n-1, -1, -1):
dp[i][i] = 1
for j in range(i + 1, n):
if s[i] == s[j]:
dp[i][j] = dp[i+1][j-1] + 2
else:
dp[i][j] = max(dp[i+1][j], dp[i][j - 1])
return dp[0][n-1]この問題に対する考え方
この問題では、以下の考え方が基本となります。
・ s = “a” の場合:“a” ができるので、最長は 1。
・ s = “aa” の場合:“aa” ができるので、最長は 2。
・ s = “bb” の場合:“bb” ができるので、最長は2。(”aa”の場合の文字が変わっただけ )
・ s = “abba” の場合:両端の文字が “a” で同じなので、 “aa”(長さ2) はできる。さらにその “a” と “a” の中には、”bb” があり、”bb” は上記の通り、長さ2はできる。よって “aa” の分と、”bb” の分を足し合わせて、2 + 2 = 4 が最長となる。
・ s = “aac” の場合:両端の文字が “a” と”c” で異なるので、(前からの)”aa” か、(後ろからの)”ac” のどちらか長い方で考える。この場合は “aa” の長さ 2 が最長となる。
また、今回のDPで、使用する配列 dp は、以下の図のように考えていきます。
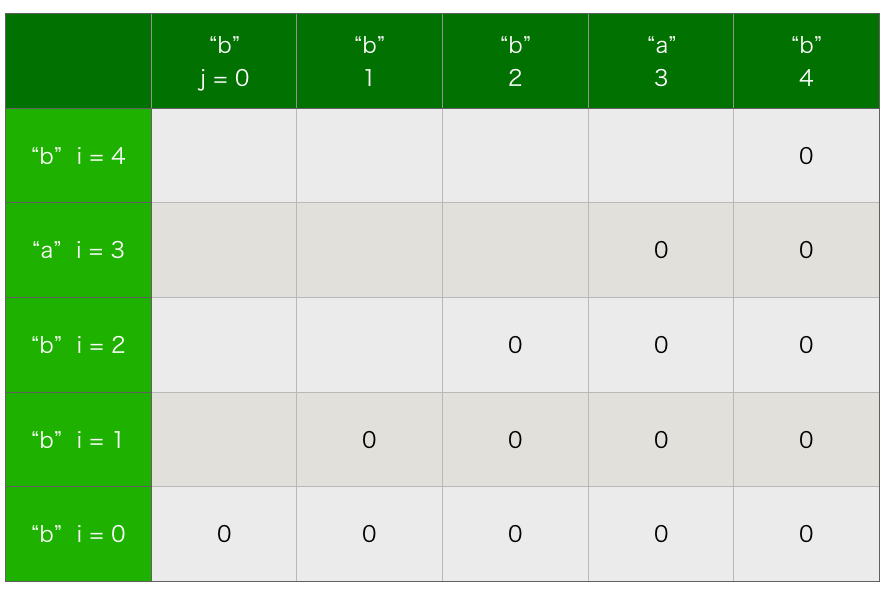
(つづく)

