LeetCodeに挑戦：63. Unique Paths II（動的計画法）

　今回は、63. Unique Paths II　に挑戦します。難易度は Medium となっています。

（問題）
　ロボットが、m x n グリッドの左上隅にいます。
　そのロボットは、任意の時点で下または右にのみ移動でき、 グリッドの右下隅に到達しようとしています。
　今、グリッドにいくつかの障害物が与えられた場合を考えます。ユニークな経路は何通りになるでしょうか？

注：m および n は最大100です。

（例）
Input: [ [0, 0, 0],
　　　　[0, 1, 0],
　　　　[0, 0, 0] ]

Output: 2
　　　
説明：3 x 3 グリッドのちょうど中央に、1つの障害物があります。右下隅に到達する方法は、
1: 右 -> 右 -> 下 -> 下
2: 下 -> 下 -> 右 -> 右　の2通りあります。

（考え方1）各グリッドへ到達可能な経路

　今回の問題では、制約条件としてロボットの移動方向が右および下の2通りのみであることに特徴がありあます。
　とりあえず障害物のことは考えない事にすれば、この制約条件により、最初の行（0行目）では、各グリッドは左側からのみ到達可能となります（図1）。

　
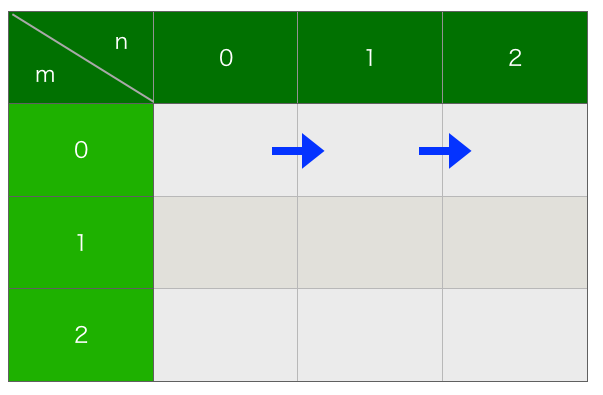
　次の行（1行目）を考えてみます。
まず、0列目のグリッドは上側からのみ訪れることができます（図2）。

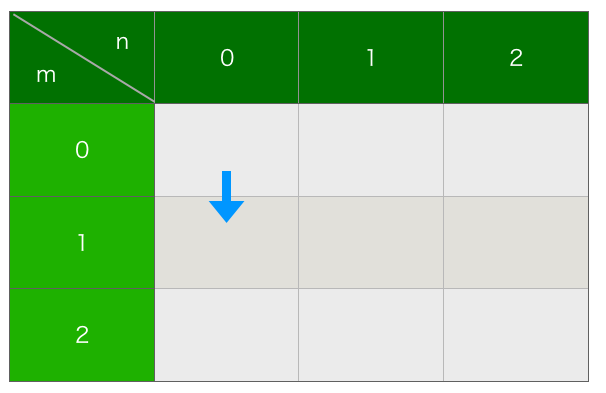
さらに、1列目以降は上側からに加えて、左側からも訪れることができます（図3）。2行目からもこれと同じ考え方になります。

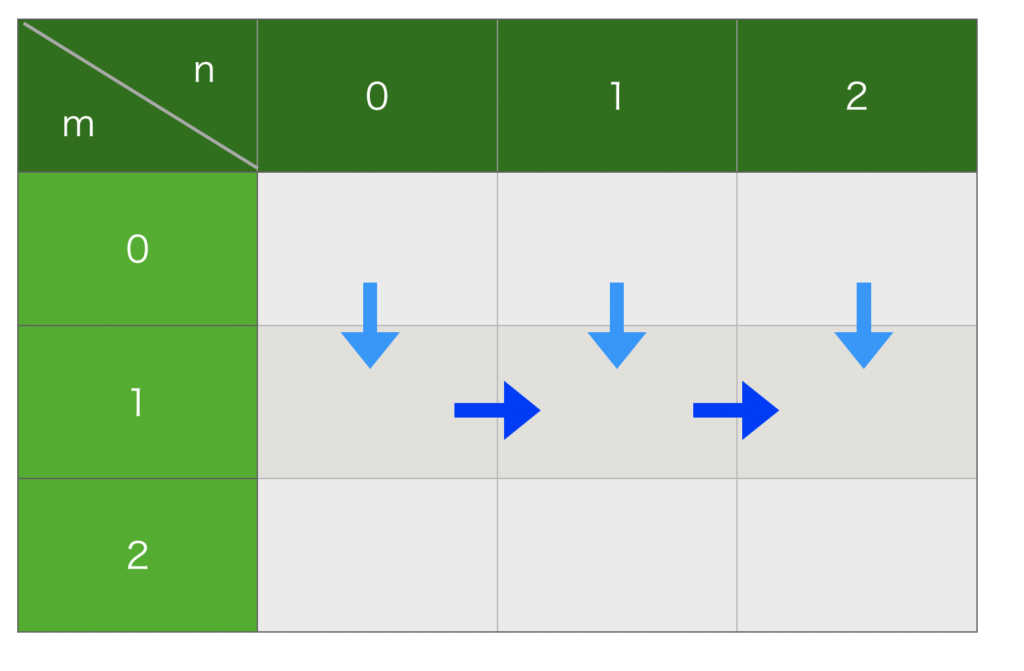
（考え方2）配列 dp の使い方

　上記の考え方をもとに、配列 dp を使って到達可能な経路を計算していく方法を考えていきます。
基本的な考え方として、与えられるグリッド（obstacleGrid）について、obstacleGrid[m][n] へ到達可能な経路の数を dp[n+1] へ書き込んで行くことにします（図4）。

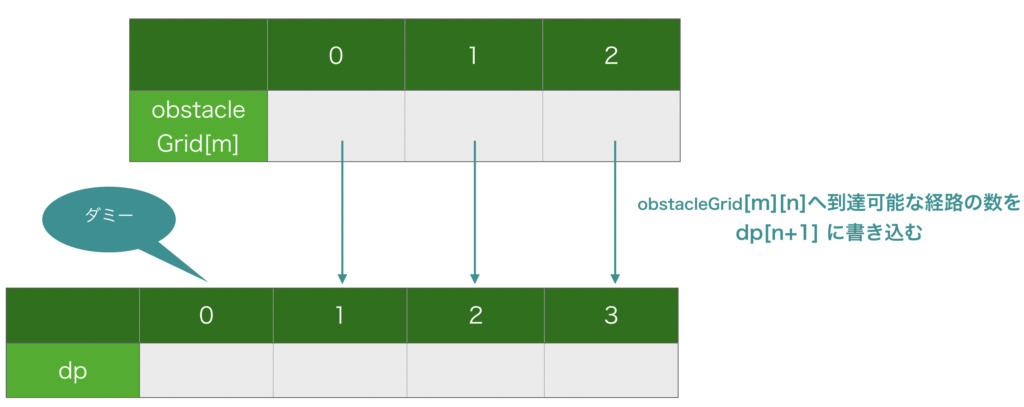
よって配列 dp の要素数は n+1 となり、図4 に示しているように dp[0] はダミーとして使用することになります。また、obstacleGrid は２次元配列で与えらえていますが、dp は1次元配列でOKです。その理由は以下で説明していきます。

（考え方3）配列 dp の初期化と obstacleGrid の０行目の処理

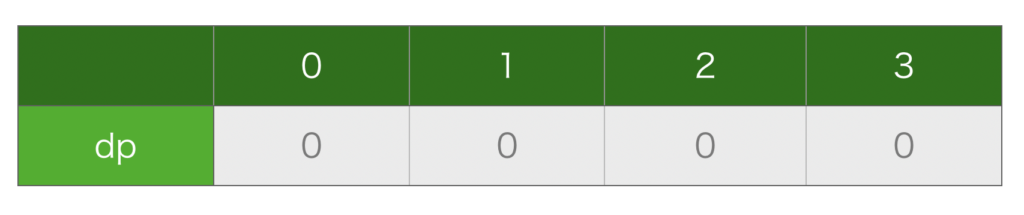
配列 dp の初期化：上で述べたように、配列 dp の要素数 n + 1 であり、またここに経路数を書き込んでいくので初期値として、0 を代入しておきます（図5）。

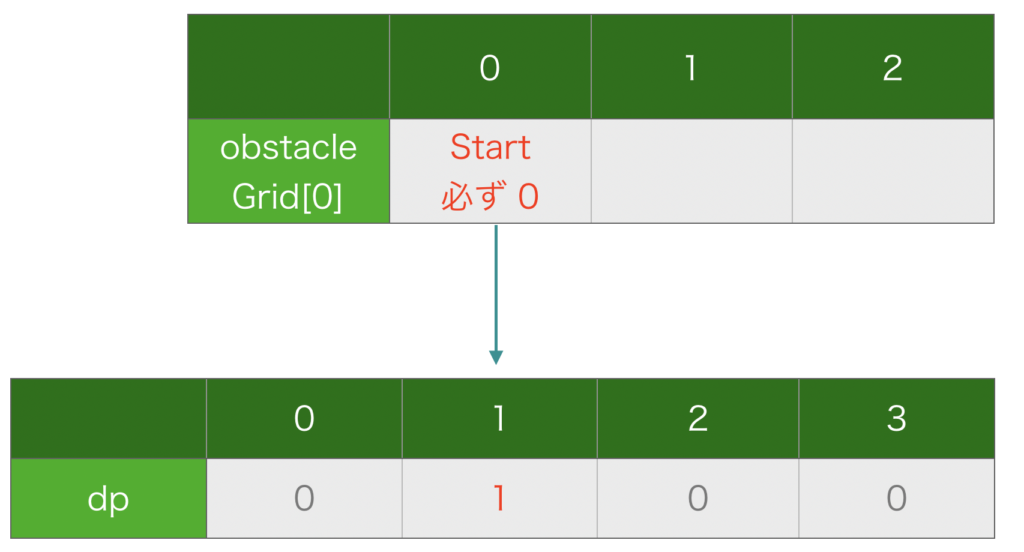
さらに、この問題ではスタート地点は左上隅、つまり obstacleGrid[0][0] と固定されているので、dp[1] = 1 となることが決まります（図6）。

右方向の処理：次に右後方へ移動していく際の処理を、obstacleGrid[0] = [0, 0, 0]　の場合と obstacleGrid[0] = [0, 1, 0] の場合に分けて考えてみます。

obstacleGrid[0] = [0, 0, 0] の場合は、すべてのグリッドを通過可能であるということです。
通過可能である場合の処理は、以下のようにすれば良いです。

if obstacleGrid[m][n] == 0:
    dp[n+1] += dp[n]

これを図にすると、図7のようになります。

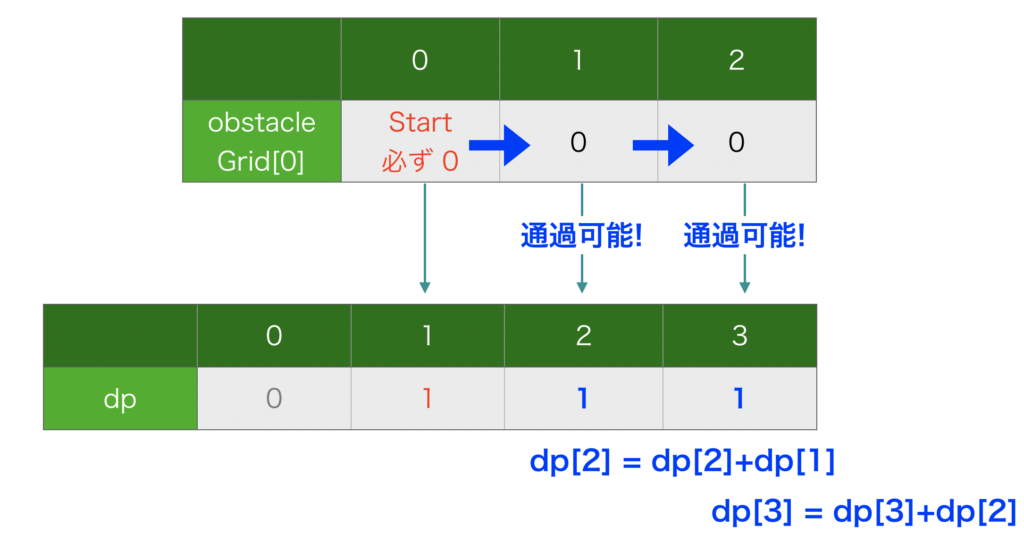
各グリッドへ到達可能な経路数が、うまく書き込まれていますね。

一方で、 obstacleGrid[0] = [0, １, 0] は、真ん中に障害物があるので、それ以降は通過できなくなっている場合です。

この場合は単純に、以下のように到達できない部分に 0 を書き込みます。

else:
    dp[n+1] = 0

これも図にすれば、図8のようになり、dp[3] は通過可能な部分ですが直前の dp[2] が通過不可能であった為、到達は不可能であるので 0 がうまく書き込めています。

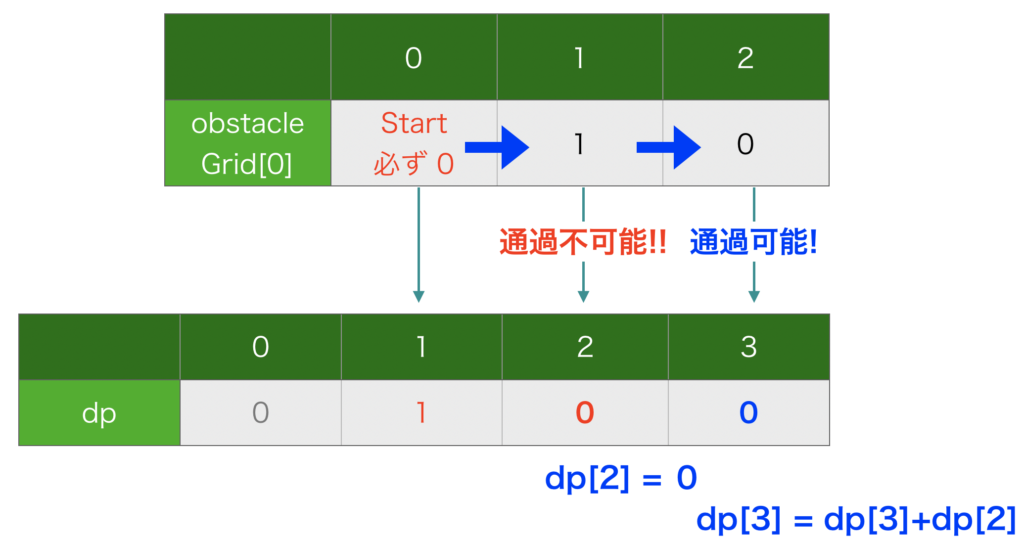
（考え方4）下方向への経路の処理

　最後に、下方向への経路の処理を考えます。
下方向への経路の処理は、特に難しいことを考えることなく、直前の行について作成した dp をそのまま初期値として引き継げば良いです。直前の行で通過可能であったグリッドはそのまま上から下方向には行けるはずですし、逆に通行不可能であった部分は行けないはずですので、そのまま引き継いで、改めて右方向の処理を行えば良い事になります。結果として、先に述べたように、 dp は1次元配列でOKとなります。

実装

最後に、これまでの考え方をもとに、python3で実装した例を以下に示します。

class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
        #(1)与えられるobstacleGridの行数の取得
        M = len(obstacleGrid)
        #(2)行数が0の場合は、0を返して終了
        if M == 0:
            return 0
        #(3)与えられるobstacleGridの列数の取得
        N = len(obstacleGrid[0])
        #dpを初期化：要素数は N+1, 初期値は 0 
        dp = [0 for _ in range(N + 1)]
        #(4)スタート地点は必ず到達可能な経路1 なので1を代入
        dp[1] = 1
        #(5) obstacleGridを探索    
        for m in range(M):
            for n in range(N):
                #(6)通過可能であれば、前のグリッドに到達可能であった経路数を足す
                if obstacleGrid[m][n] == 0:
                    dp[n+1] += dp[n]
                #(7)通過不可能であれば0を記入
                else:
                    dp[n+1] = 0
        #(8) dpの最後が、obstacleGridの右下に対応するので、その値を返して終了             
        return dp[-1]