プログラミングコンテストでは、ある(無向)グラフが与えられ、
その中の2つの頂点(ノード)を結んだ場合に、そのグラフが閉路(ループ)を持つことになるか?
を判定しなければならない問題が出題されることがあります(たとえば AtCoder Beginner Contest 231 D問題 など)。
その閉路の検出は、UnionFind を用いることで簡単に行うことができます。
例として、以下の2つのグラフでは、
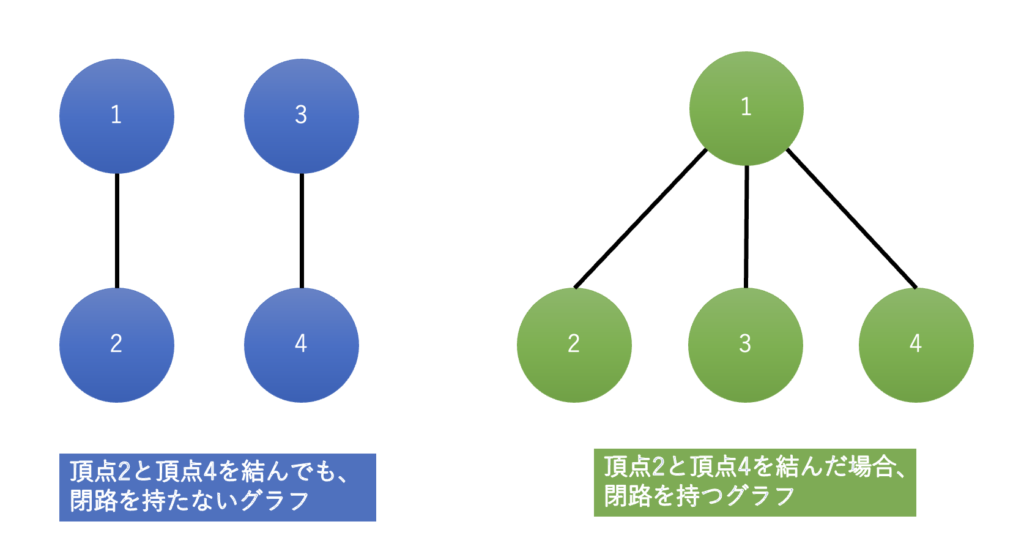
青色のグラフでは、頂点2と頂点4を結んでも、1 – 2 – 4 – 3 という並びになるだけで閉路は持ちません。
一方で、緑色のグラフは頂点2と頂点4を結ぶと、1 – 2 – 4 の中で閉路(ループ)が発生します。
そのように、ある2つの頂点を結んだ場合に閉路ができるかどうかを判定する方法を、
UnionFind を使って、python3 で実装してみます。
UnionFind
今回使う UnionFind のコードは以下の通りです。
#今回の例で使用する頂点の数
N = 4
#各頂点(要素)の根(親)を管理する配列:初期値は各頂点自身, 頂点数は上述の N
root = [i for i in range(N+1)]
#各頂点(要素)の高さを管理する配列:初期値は最下位の0
rank = [0]*(N+1)
#頂点xの根(親)を見つける関数:戻り値は根(親)の頂点番号
def find(x):
#print(x, root)
if root[x] == x:
return x
else:
root[x] = find(root[x])
return root[x]
#頂点xと頂点yが同じ根(親)を持つかを判定する関数:戻り値はBoolean(True or False)
def same(x,y):
return find(x) == find(y)
#頂点xと頂点yが所属するグループを併合する関数
def unite(x,y):
x = find(x)
y = find(y)
if x == y:
return 0
#浅い(木の高さとして低い)方を深い(高い)方に合併
if rank[x] < rank[y]:
root[x] = y
else:
root[y] = x
if rank[x] == rank[y]:
rank[x] += 1
上記コード中の関数、unite(x, y) を使って、与えられたグラフを表現するために、頂点を結合していきます。
今回の「閉路を持たないグラフ」の例では、
unite(1,2)
unite(3,4)と記述することになります。
一方で、「閉路をもつグラフ」の例では、
unite(1,2)
unite(1,3)
unite(1,4)
と記述します。
閉路の判定
今回は、頂点2と頂点4を結んだ場合に閉路が発生するかを調べたいのですが、
これは言い換えれば「頂点2と頂点4が同じ根(ルート)を持っているか?」を調べることになります。
同じルートを持つ2頂点を結べば、閉路が発生することになり、
異なるルートを持つ2頂点を結んでも、閉路は発生しない訳です。
よって実際のプログラムは、
same(2, 4)と記述すれば、
「閉路が発生する = 同じルートを持つ」場合は「True」が返され、
「閉路が発生しない = 同じルートを持たない」場合は「False」が返されます。
割と簡単ですね。
それでは最後に、それぞれのケースのコード全体を載せて終わりたいと思います。
お役に立てれば嬉しいです。
(例)頂点2と頂点4を結んでも平路を持たないグラフ
#今回の例で使用する頂点の数
N = 4
#各頂点(要素)の根(親)を管理する配列:初期値は各頂点自身, 頂点数は上述の N
root = [i for i in range(N+1)]
#各頂点(要素)の高さを管理する配列:初期値は最下位の0
rank = [0]*(N+1)
#頂点xの根(親)を見つける関数:戻り値は根(親)の頂点番号
def find(x):
#print(x, root)
if root[x] == x:
return x
else:
root[x] = find(root[x])
return root[x]
#頂点xと頂点yが同じ根(親)を持つかを判定する関数:戻り値はBoolean(True or False)
def same(x,y):
return find(x) == find(y)
#頂点xと頂点yが所属するグループを併合する関数
def unite(x,y):
x = find(x)
y = find(y)
if x == y:
return 0
#浅い(木の高さとして低い)方を深い(高い)方に合併
if rank[x] < rank[y]:
root[x] = y
else:
root[y] = x
if rank[x] == rank[y]:
rank[x] += 1
unite(1,2)
unite(3,4)
print(same(2,4))
# --> False
(例)頂点2と頂点4を結ぶと平路を持つグラフ
#今回の例で使用する頂点の数
N = 4
#各頂点(要素)の根(親)を管理する配列:初期値は各頂点自身, 頂点数は上述の N
root = [i for i in range(N+1)]
#各頂点(要素)の高さを管理する配列:初期値は最下位の0
rank = [0]*(N+1)
#頂点xの根(親)を見つける関数:戻り値は根(親)の頂点番号
def find(x):
#print(x, root)
if root[x] == x:
return x
else:
root[x] = find(root[x])
return root[x]
#頂点xと頂点yが同じ根(親)を持つかを判定する関数:戻り値はBoolean(True or False)
def same(x,y):
return find(x) == find(y)
#頂点xと頂点yが所属するグループを併合する関数
def unite(x,y):
x = find(x)
y = find(y)
if x == y:
return 0
#浅い(木の高さとして低い)方を深い(高い)方に合併
if rank[x] < rank[y]:
root[x] = y
else:
root[y] = x
if rank[x] == rank[y]:
rank[x] += 1
unite(1,2)
unite(1,3)
unite(1,4)
print(same(2,4))
# --> True