プログラミングコンテストでは、「ある数列の中から任意の数字を選び出し、目的とする数(S)ができるか?」といった、いわゆる部分和問題が多々出題されます。
部分和問題では、制約条件や出力形式を変化させることで様々なバリエーションが存在しますが、ここでは以下の条件の部分和問題を紹介します。
・正の数列が与えられる
・目的とする数 S が与えられる
・数列の中の数字は1度のみ使用できる
・出力は、「True(できる) or False(できない)」のいわゆる boolean とする
以上の制約条件の中で、数列 mylist = [1,2,5,8] 、目的とする数 S = 10 の場合を動的計画法(DP)を用いて、python3で解く方法を以下に紹介します。
コード全体
さっそく、以下にコードの全体を示します。
# (1)
S = 10
mylist = [1,2,5,8]
mylist = [0] + mylist
N = len(mylist)
# (2)
dp = [ [0 for i in range(S+1)] for n in range(N)]
dp[0][0] = 1
#(3)
for i in range(1,N):
for j in range(S+1):
if j >= mylist[i]:
dp[i][j] = dp[i-1][j-mylist[i]] or dp[i-1][j]
else:
dp[i][j] = dp[i-1][j]
#(4)
if dp[-1][-1]:
print(True)
else:
print(False)上記コードを個別にみていきます。
(1) 初期条件
あらためて、この問題は数列 mylist の中の各要素を選び(ただし各要素の使用回数は1回)、目標とする数 S ができるかを問うものなので、それらをここに記述しています。
また、以降の記述を分かりやすくするため、mylist の要素として、先頭に 0 を加えています(0 を加えなくてもできる方法もあります)。
その上で、以降の for ループで使用するため、mylistの要素数を N = len(mylist) として取得しています。
(2) 配列dpの初期化
S ができるかどうかを、 boolean として記述する配列 dp を用意します。
ここで dp の要素数は dp = [[0 for i in range(S+1)] for n in range(N)] と記述しています。これを説明するために、その全体像を図1に示します。

まず、列を示す range(S+1) については、0 から S までの要素数を持たせています。これは、あくまで目標は S ですが、そこに至るまでを 0 から順に考えていくためです。
一方で、行を示す range(N) については、mylist の要素数を持たせています。これは 図1 の中に書いている通り、行方向では、はじめに mylist の要素を1つだけ(例では 0を)使って、0 から S までの数をつくることができるかを考えます。その後は、mylist の中の次の要素と前までの要素のを使って、同じように 0 から S までの数をつくることができるかを考えます。
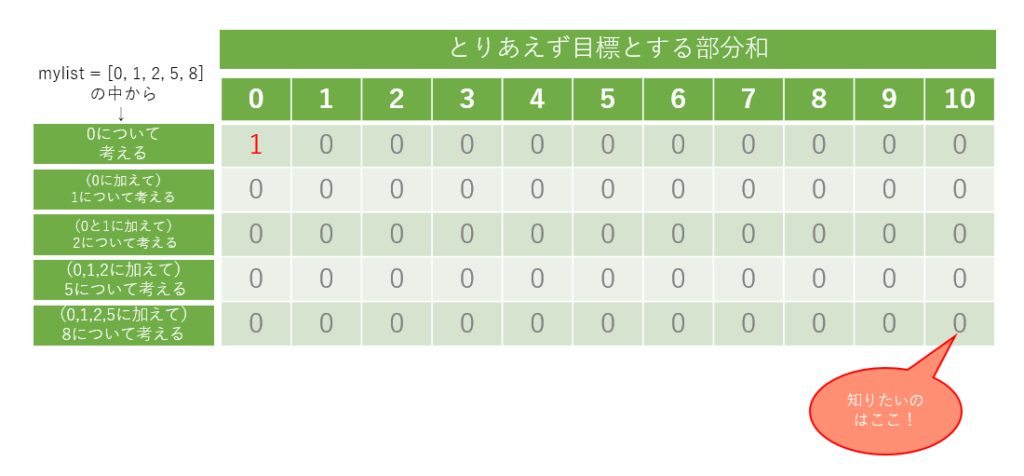
さらに初期値としては、とりあえず全体に 0 を与えた上で、dp[0][0] = 1 としています。dp[0][0] は、 mylist の 要素 0 を使って 0 がつくれるか?を調べているところで、当たり前につくることができるからです。初期化後の dp について 図2 に示します。
(3) 部分和の探索
(3) の部分でいよいよ部分和を探索していきます。ここでは 2重の for ループを用いて各列を順に探索していきます。
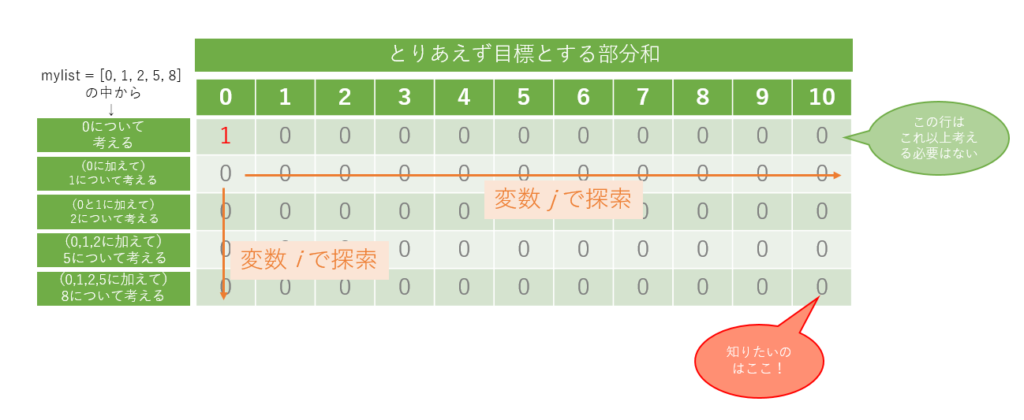
この時、行方向に対する for ループは for i in range(1,N): と記述しているように、1 から開始しています。これは先に述べたように、i = 0 の行については、 0 を使ってできる数字を探索している行であり 0 しかつくれませんので、それ以上の探索は不要です。さらに、後に述べるようにここで使用している探索方法は、前の探索結果を参照するようにしています。よって、前の探索結果が既にある状態から探索をはじめる必要があります。以上の内容について図3に示します。
if j >= mylist[i]: の部分からがこの探索の肝となります。この if 文は 「 j で見ている数字が、 今見ている mylist[i] の要素以上の数の場合は」という内容の判定文です。例えば、 j = 3 で、mylist[2] = 2 の場合を考えると、3 をつくるために 2 を用いた場合は、1を加える余地があります。
そのような理由で、 j >= mylist[i]: が重要となります。その判定分にかかる部分を、図4 にオレンジ色で示します。
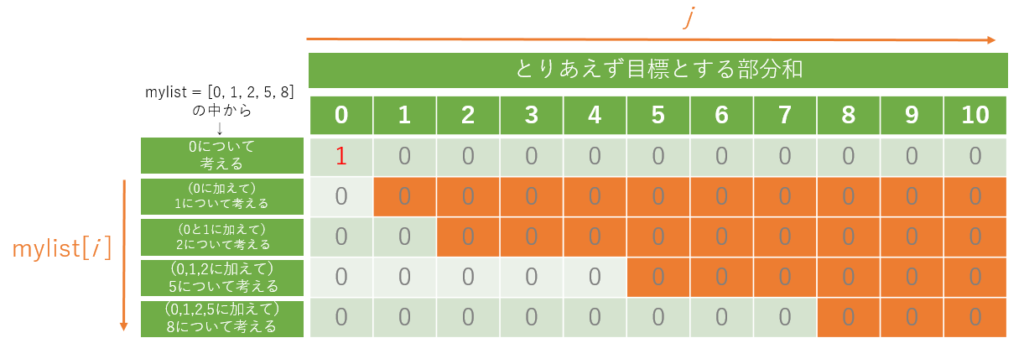
実際の探索の順序で見ていくと、
i = 1、j = 0 の場合は mylist[1] = 1 は 0 より大きいので、判定文にはかからず、else 側の
dp[i][j] = dp[i-1][j] にまわります。これは、以前の行の結果をそのままもってくることを意味しています。このようにすれば 1 で 0 をつくることができなくても、既に 0 で 0 をつくることができたているので、その結果をうまく持ち越すことができます(図5)。
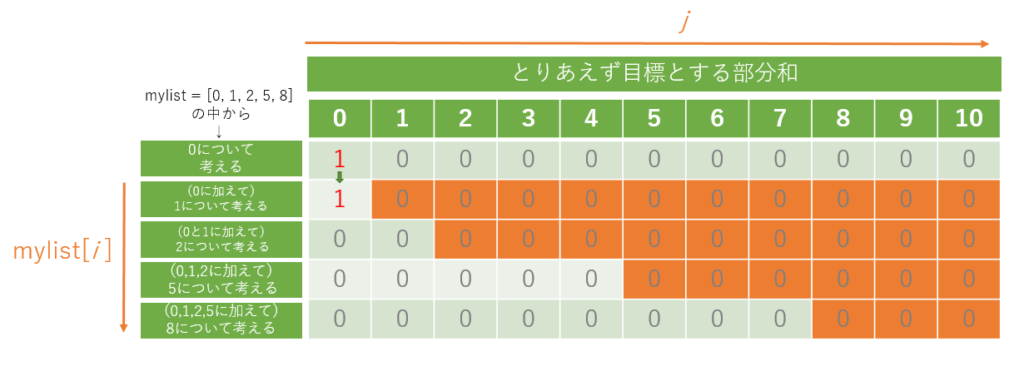
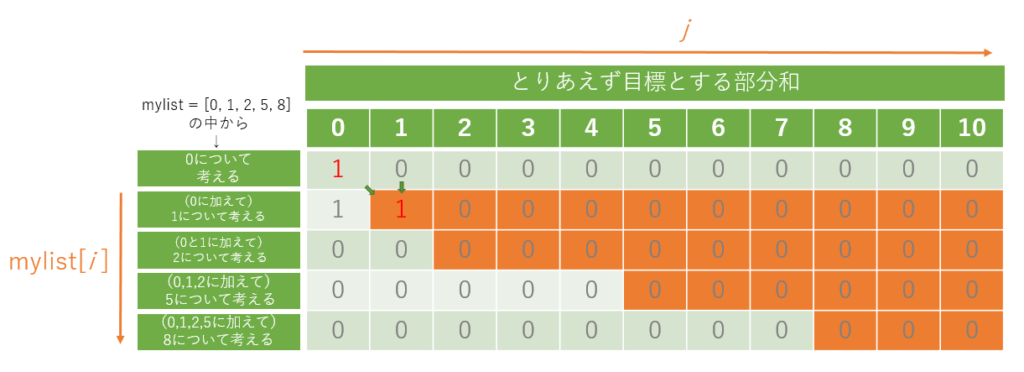
次に、 i = 1、j = 1 の場合は mylist[1] = 1 は 1 以上となるので、判定文にかかり、 dp[i][j] = dp[i-1][j-mylist[i]] or dp[i-1][j] の処理となります。
この記述では or を用いています。これは dp[i-1][j-mylist[i]] が True(= 1)ならば dp[i][j] = 1 となり、 dp[i-1][j-mylist[i]] が False(= 0)ならば dp[i][j] = dp[i-1][j] となるように処理されます。
現在の例では、 dp[i-1][j-mylist[i]] = dp[0][0] = 1 となっているので、 dp[i][j] = dp[1][1] = 1 となります(図6)。
(4) 最終出力
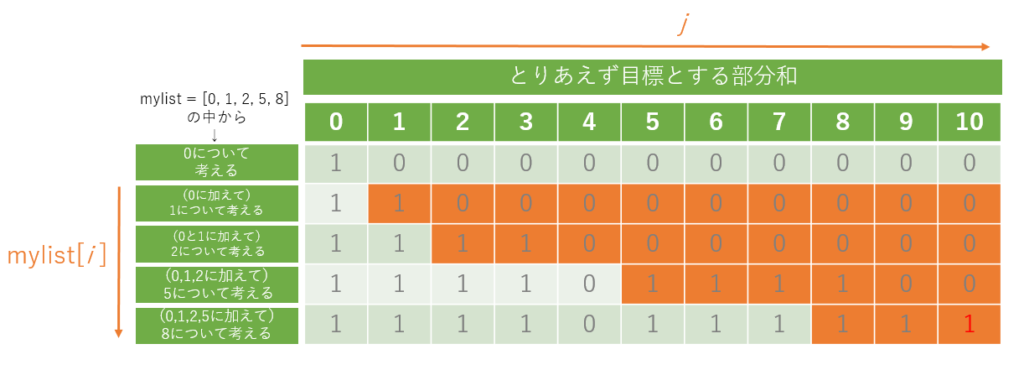
以上の処理を終えると dp は 図7 のようになります。
この配列の末端 dp[-1][-1]が mylist の要素すべてを使って S ができるかどうかを記述している部分でしたので、そこをみると 1 となっており、Sはつくることができることになります。それについて(4) の部分で処理し出力しています。
動的計画法は、私自身も苦手ですぐには実装できないことが多いのですが、表をもとに考えていけば何とか理解はできるかとおもいます。
